中学生の代数で手が止まる原因と定期点数を上げる計算・解法習得法
wpmasterまず1分で結論：代数で手が止まる3原因と、今日やる練習順
代数で止まりやすい「つまずきパターン」
- 計算が遅い（正確さが安定せず、スピードに移れない）
- 途中式（式変形）を省いてミスが増える（見直しで原因が追えない）
- 因数分解などで「知っている基本形」が少ない（少し形が変わると止まる）
今日の練習順（迷ったらこの順で）
- 正確に書ける（途中式を1行ずつ残し、ミスの場所が見える状態にする）
- だんだん速くする（同じ解き方を反復して「考える時間」を減らす）
- 知っている形を増やす（因数分解などは“基本パターン”を覚える→使う→反復）
速さは最後で大丈夫です。まずは「正しく解ける書き方」で残すほど、結果的に速くなりやすいです。
途中式テンプレ：移項・分母払い・約分を「1行ずつ」
ここは“見た目の丁寧さ”が点数に直結しやすいところです。最初は省略しない書き方を徹底し、慣れてから少しずつ短くしていきます。
例題① 移項（符号ミスを止める書き方）
2x + 7 = 3 2x = 3 - 7 2x = -4 x = -2
- 「移項＝反対側に引っ越す」より、「両辺から7を引く」と書く方が符号ミスが減りやすいです。
例題② 分母払い（両辺を何倍するかを残す）
x/3 + 1/2 = 5/6 （両辺×6） 2x + 3 = 5 2x = 2 x = 1
- 「両辺×6」を必ず一度書くと、途中で何をしたかが乱れにくいです。
- 掛け算が終わってから移項、の順にすると混乱が減ります。
例題③ 約分（“割れる因数”を先に見つける）
6x/9 = 2/3 （左辺を約分） 2x/3 = 2/3 （両辺×3） 2x = 2 x = 1
- 約分は「割れる数を見つけてから」一段ずつ。頭の中でまとめてやらない方が安全です。
- 慣れるまでは、約分→両辺操作（×3など）を分けて書くのがおすすめです。
因数分解の“基本パターン”チェックリスト：基礎レベル→追加すべきパターン
基礎レベル（まずはここが不安なくできるか）
- □共通因数でくくる（例：ax + ay = a(x + y)）
- □平方差（a² − b² = (a + b)(a − b)）
- □完全平方（a² ± 2ab + b² = (a ± b)²）
「まずくくる」「a²−b²っぽいか」「(a±b)²っぽいか」を順に確認すると、見落としが減りやすいです。
追加すべきパターン（ここが増えると“見たことある形”が増える）
- □2つずつのまとまり（グループ分け）（例：ax + ay + bx + by → (a + b)(x + y)）
- □x² + bx + c 型（かけてc、足してb を探す発想）
- □ax² + bx + c 型（係数が1でないときのまとめ方）
「知っている公式」だけで押し切ろうとすると止まりやすいので、“解き方のバリエーション”を少しずつ増やしていくのが近道になりやすいです。
振り返り（使ったパターンにチェックして、次の復習を短くする）
| 問題 | 使ったパターン（チェック） | 次回の注意点 |
|---|---|---|
| 例：① | □ くくる □ 平方差 □ 完全平方 □ グループ分け □ x²+bx+c □ ax²+bx+c | （符号／係数／見落とし など） |
| 例：② | □ くくる □ 平方差 □ 完全平方 □ グループ分け □ x²+bx+c □ ax²+bx+c | （途中式を残す／先にくくる など） |
| 例：③ | □ くくる □ 平方差 □ 完全平方 □ グループ分け □ x²+bx+c □ ax²+bx+c | （同じパターンをもう1問 など） |
「どの解法を使ったか」を残しておくと、復習が“当てずっぽう”になりにくく、反復の効率が上がりやすいです。
代数分野が苦手な生徒に共通するポイント
代数分野が「なかなかできない」と感じている生徒さんには、次のような共通点が見られます。
- 計算スピードが遅く、テストで時間が足りなくなる
- 途中の式変形を省いてしまい、ミスに気づけない
- 因数分解などを最低限の公式だけで乗り切ろうとする
- いろいろな問題パターンに触れておらず、応用になると手が止まる
逆に言えば、これらのポイントを押さえて勉強していけば、代数分野は必ず得意にしていくことができます。
計算スピードを上げるトレーニング
まずは「正確さ」を優先して計算に慣れる
代数分野が苦手な生徒さんに共通しているのが、計算スピードが遅いという点です。特に、小学校で学習する分数の四則計算で手間取ってしまうと、
- 定期テストで全問解き終わらない
- 後半の応用問題にたどり着けない
といった状況になりがちです。 計算スピードを上げるためには、まず
- たくさんの計算問題に触れ、計算そのものに慣れること
- 最初のうちは「速さ」よりも「正確さ」を重視すること
が大切です。計算への抵抗感が薄れてきたら、徐々に「同じミスを減らしながらスピードを上げる」ことを意識していきましょう。
スピードアップがもたらすメリット
計算スピードが上がると、
- 定期テストで全問にしっかり取り組む時間的余裕が生まれる
- 見直しの時間を確保でき、ケアレスミスも減らせる
といったメリットがあります。代数分野を得意にするためには、まず計算をスピーディーに処理できる土台を作ることが不可欠です。
式の変換（式変形）を省かない習慣をつける
途中の式を書かないと、ミスに気づけない
「速く解こう」と意識するあまり、途中の式変形をノートに書かない生徒さんも少なくありません。特に、
- 両辺を10倍するとき
- 文字を移項するとき
などで、学校の先生が黒板では計算を省略して進めることも多く、それをそのまま真似してしまうケースが見られます。 しかし、式を省略してしまうと、
- 頭の中での処理があいまいなまま進んでしまう
- 途中で誤った計算をしても、計算過程が残らないため見直しでミスに気づけない
といった問題が起こります。
「丁寧に書く → 徐々に省略」の順番で
計算が苦手な場合は、まずは丁寧に式を書くことを徹底しましょう。
- 最初から暗算で処理しようとせず、式の変換を一行ずつ書いていく
- 移項・約分・両辺を何倍するかなど、一つひとつ目に見える形で残す
こうしたステップを踏んで計算が身についてきたら、
- 移項など、ミスが少ない部分から少しずつ省いていく
- 省略しても正解できるようになってきた段階で、初めて「スピード」も意識する
という流れで、「正確さ」と「速さ」のバランスを調整していくとよいでしょう。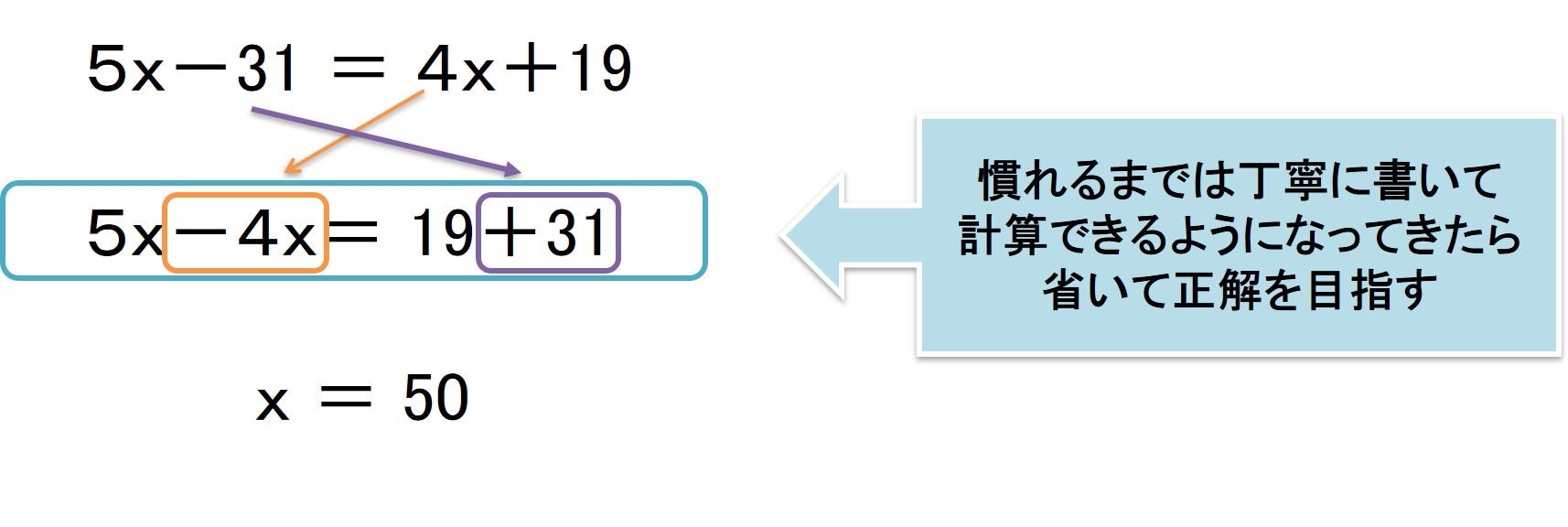 
ポイントは、集中力を切らさずに最後まで手を動かし続けることです。途中式を書きながら計算する習慣がつけば、ミスも減り、結果として効率の良い学習につながります。
公式に頼りすぎない「知識の厚み」をつくる
最低限の公式だけでは、解ける問題が限られる
代数分野が苦手な生徒さんは、特に因数分解などで、最低限の公式だけでなんとか乗り切ろうとしてしまう傾向があります。しかし、
- パターンが少ないと、少しひねった問題が出たときに太刀打ちできない
- 「見たことのない形」に感じてしまい、手が止まってしまう
といった状況に陥りがちです。 「知っていればできる」タイプの問題は、ある程度覚えることが必須です。公式や代表的な変形パターンは、
- 「覚える → 使う → 反復する」
というサイクルを通して、自分の武器にしていく必要があります。
さまざまな問題に触れて「使える知識」にする
知識を増やしていくためには、
- 基本問題だけでなく、少しずつレベルの違う問題にも挑戦する
- 問題ごとに「どの公式・どの考え方を使ったのか」を意識する
- 同じパターンの問題を、解けるまで何度も反復する
といった取り組みが重要です。 演習を重ねていくと、
- 問題を見た瞬間に「このパターンはこの解き方だ」と自然に判断できる
- 「代数はもう怖くない」と感じられる場面が増えてくる
ようになります。そのためにも、まずは計算力という土台をしっかり高めつつ、知識の幅も少しずつ広げていきましょう。
当塾での取り組み：代数分野を得意にする個別サポート
当塾では、中高一貫校生を対象に、次のような学校対策を行っています。
- 授業の先取りを行う「先取りコース」
- 既習内容の理解を深める「フォローアップコース」
生徒さん一人ひとりの状況に合わせて、もっとも効果的なカリキュラムを作成し、完全オーダーメイドの授業で代数分野の強化を行います。 また、中高一貫校で多く採用されている体系数学の対策も行っており、教科書ごとの特徴やカリキュラムの進度に合わせた指導が可能です。 さらに、当塾では教室と同様の授業をオンラインでも受講できます。
- 通塾の必要がなく、移動時間を学習時間に充てられる
- 自宅など、勉強し慣れた環境で授業を受けられる
など、忙しい中高一貫校生にとっても学びやすい環境を整えています。
まとめ：代数分野を得意にするためのポイント
代数分野が苦手だと感じている場合も、取り組み方を変えることで状況は必ず変わります。最後に、この記事のポイントを整理しておきましょう。
- まずは計算スピードと正確さを上げるために、日々計算問題に取り組む
- 苦手な計算や移項などは、式を丁寧に書き出して徐々に慣れていく
- 因数分解などは、最低限の公式だけでなく、必要な知識を幅広く覚える
- さまざまな問題に触れて、出題パターンと解き方をセットで身につける
- 代数分野は、計算の処理能力を上げること＋覚えるべきことを覚えて活用できるようにすることが何より大切
また、幾何分野が苦手な方は、『数学(幾何分野)が中々出来ない生徒さん向けの勉強法』もあわせてご覧いただき、代数分野・幾何分野の両方をバランスよく伸ばしていきましょう。
代数計算を「ただの作業」と捉える限り、合格への道は遠のきます。
意味を理解しない丸暗記の解法が癖になると、記述式での容赦ない減点が積み重なり、合格を左右する合計点に跳ね返る致命的な不利益を被ります。
努力が得点に反映されない本質的な理由は、一重に判断基準が定まっていないことにあります。
講座案内：受験対策 医学部対策講座【英語・数学】
基本的な英語の学力をつけた上で、大学別の対策を実施します。解答作成に必要な文章構成能力など総合的に養成します。【数学】
医学部受験では、典型問題までは確実に解答していく力が求められますので、 合格に必要な実力を身に付けていくための学習計画を立てるところから指導させていただきます。
講座案内：ワンポイント講座 国文法ワンポイントゼミ【国語】
現代語の文法は古文の文法学習をするための準備として位置づけられていますので、定期試験対策としての受講だけでなく、古典文法の学習準備として中学生が受講することも歓迎しています。
